回転とはある点における単位面積あたりの渦(「」参照)の強さの量です。
言い換えると、渦を起こす何らかの物があると考えて、それの密度が回転です。
流体の中で何かを回転させるとそこに渦が出来ますから、ベクトル場の渦を作るこの力のことを回転と言うわけです。
すなわち、ある点Pにおけるベクトル場
F
の回転
rot
F
とは、点Pを通る任意の曲面をS、その外周をl、Sの点Pにおける法線を
n
とすると、Sの取り方によらず常に
が成り立つベクトルです。
また、
rotφ
は
∇×φ
とも書きます
。
これだけでは分かりにくいでしょうからもう少し直感的な回転の意味を言うと、
回転とは
線積分(「線積分とは」参照)と面積分(「面積分とは」参照)を関係付ける微分演算
で、直交座標を用いて表すと
となります。
ただし、
F = (
Fx, Fy, Fz
)
です。
∇×
F
という書き方をするのは、ナブラベクトル
∇ = (
,,
)
と
F
の外積を取ったものが回転となるからです。
いきなり3次元の線積分と面積分を関係付ける公式を出すよりも、2次元で考えたほうが分かりやすいので、まずは2次元で考えます。
図1のような積分経路を考えると、ベクトル場
F
の線積分の値は
{
Fy(x+dx,y)−Fy(x+,y)
}
dy − {
Fx(x,y+dy)−Fx(x+,y)
}dx
となります。
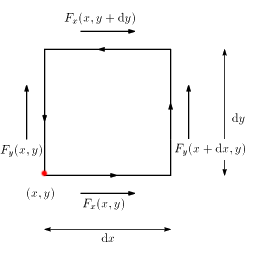 積分経路
積分経路
ここで、
Fy(x,y)−Fy(x+dx,y) = dx
であることを用いると、この式の第一項は
dxdy
となります。
同様に第二項も
dxdy
となりますので、この線積分の値は
となります。
すなわち、
が成り立ちます。
この式をグリーンの定理といいます。
回転は単位面積あたりの渦の強さなわけですから、回転の面積分の値は渦の強さに等しくなります。
つまり、
この式をストークスの定理といい、線積分と面積分を関係付ける公式です。
この面積分の値をx方向成分、y方向成分、z方向成分に分けて考えます。
x方向成分は曲面Sをy−z平面に投影したものを考えればいいので、
2次元の場合と同様にグリーンの定理を使って
∫∫{
−
}dydz
とあらわすことができます。
同様に、y方向成分、z方向成分はそれぞれ
∫∫{
−
}dzdx
、
∫∫{
−
}dxdz
となります。
これらを足し合わせたものが面積分の値になりますので、
∮
F・
dl =
∫∫[
{
-
}dy
dz
+
{
-
}dz
dx
+
{
-
}dx
dz
]
∴
∮F・dl =
∫(
-
,
-
,
-
)
・dS
となります。そして回転の定義より、
となります。

