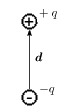電場と電束密度
電荷の作る場には、電場と電束密度という2つのものがあります。 どっちも似たようなものなのに、なぜ2つあるのかって疑問をもたれるかたもいるかと思います。 あと、似ているようで微妙に違ってて混乱したりも。 そういうわけでここでは電場と電束密度について解説していきます。
電場というのは、2つの電荷の間に働く力を近接作用で考える(つまり、電荷が存在するところには何らかの場が発生して、その場が他の電荷に力を加えると考える)際に利用する場です。 すなわち、電荷の周りには電場が発生し、電場 E の中に電荷qをおくと、
という力が発生するするというものです。
一方で、 電束密度は自由電荷を湧出点とする「流束」 です。 つまり、自由電荷密度分布が ρ のとき、
を満たすような場 D が電束密度です。
そして、この2つの量の間には比例関係が成り立ちますから、比例係数 ε0 を定義して
という関係が成り立ちます。 ここで用いた比例係数 ε0 を 真空中の誘電率 といいます。
誘電体
誘電体とは、電場をかけると分極を起こして分極電荷の現れる物質のことです。
分極とは、誘電体中に負電荷(電子)と正電荷(原子核)の位置が微妙にずれたもの(これを電気双極子という。左図参照。)が分布した状態のことを言います。 誘電体に電場をかけることで、原子核と電子の位置がずれ、このような状態が生じます。 このような、電気双極子の分布によって電荷の分布が生じます。 この分極によって生じる電荷分布を分極電荷といい、 分極の変化によって生じる電流密度分布を分極電流密度といいます。
電気双極子に対して、電気双極子モーメント p というものを定義し、
で表します。 ここで、qは双極子を作る電荷の電気量で、 d は正負の電荷の間の位置の差を表すベクトルです。 なぜこの式で電気双極子を表すかというと、このような電気双極子に対して電場 E をかけると、電気双極子を電場と同じ向きに向けようとするトルク(偶力) T がはたらき、 T = p×E と表せるからです。
次に、分極は電気双極子の密度ですから、電気双極子の分布密度をNとすると、 分極密度 P は
となります。
そして、分極によって生じる分極電荷 ρ p は
となり、分極の変化によって生じる分極電流密度 J p は
となります。(電束密度と電荷、電流の関係とは符号が逆なのに注意。)
誘電体中の電場・電束密度
電束密度 D は自由電荷(つまり、誘電体に生じた分極電荷は考慮に入れない)から湧き出してくる流束です。 要するに、電束密度は誘電体中でもその値は変わりません。 また、誘電体に電場をかけると分極 P が生じます。 この様子を下図1、2に示します。
一方、電場 E は、電荷にかかる正味の力をあらわすものですから、 誘電体に生じた分極の分まで考慮に入れる必要があります。 すなわち、誘電体中では電場は変化し、
という関係が成り立ちます。 この様子を下図に示します。
|
|
|
|
さて、ここで分極密度が誘電体にかけた電場に等方線形時不変で比例すると仮定します(この仮定はどんな誘電体に対しても出来るわけではありませんが、たいていは出来るものとみなして大丈夫です)。 この仮定の元、 E = χeε0P と置くと、
となります。 ここで用いた比例係数 χe を分極率といい、 ε を(誘電体中の)誘電率といいます。 また、 εr = 1+χe というものを定義し( ε = εrε0 )、これを比誘電率といいます。